予科の算数で躓いた

図形得意なの！とか言っていた娘だけれど、今回の授業・・・・面積で躓いたみたいです。学んだことを使うが終わってない！
今週は私が教えなければなりませんでした。
というよりも、私もテキストの解答を見てもよくわからない・・・考え方とか単元のねらい間違って教えてないか不安・・・
EXCELでジオボードを作って適当に遊ばせてみます。色塗りは大好きみたいで食いつきはいいですが、理解はできていないようです。まずは興味をそそらせるためのEXCELで色塗りです。




食いつきはいいのですがやはりできないですね。興味を持ってくれたのでEXCELで作ったジオボードを印刷し、手書きさせました。
好きに書いていいよ。面積が20c㎡になる正方形書いてね！
といってもどうかけばいいのかわからないらしく、時間をかけたけど手は動かず。
仕方ないのでまずはテキストの解答にあるように1辺が4cmの正方形よりも、1辺が少しだけ長い正方形を書くには、斜めにすればいいよね！ということで１つ斜めに。1つ斜めだと17c㎡なので、じゃあ、もうひとつ斜めにして1辺を長くしよう！
やり方が分かったらしく、いくつかの正方形を10ページくらいのジオボードにひたすら書いてました。

描画の仕方を学ぶのが目的とは思えないのですが、手を動かして描いた正方形の面積を求めることもあるので、ひたすら書かせました。

他にもやり方があると思いますが、メモということで。
例えば、面積が25c㎡で、周りの長さがもっとも短い長方形を書きましょう！という問題です。
面積25c㎡なら5ｘ5の正方形を書けばいいだけですね。

こんな簡単でいいのでしょうか？もっと深く考えてもらいましょう。正方形を傾けて斜めにするのです。
25c㎡は3ｘ3＝9c㎡の正方形と16c㎡の周りの枠で構成されています。

16c㎡は4ｘ4なので、25c㎡の正方形は下図のように3ｘ3＝9c㎡の正方形と4ｘ4＝16c㎡の正方形を合わせた面積に等しいことがわかります。

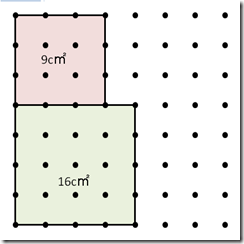
重ねると縦は7cm必要です。横を7cmまで広げ、二つの正方形を囲む正方形を作ります。4c㎡の１辺は3cm、16c㎡の1辺は4cmです。2つの正方形を囲んだ正方形の1辺は7cmです。7cmは3cmと4cmで分けられています。

正方形の左上の角から右へ3cmの位置、左上の角から下へ4cmの位置を結ぶ直線を引きます。

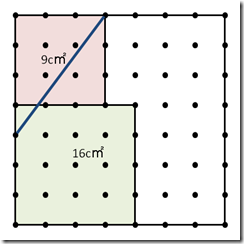
今度は正方形の左下の角から上へ3cm、左上の角から右へ4cm位置を結ぶ直線を引きます。

あとは繰り返しです。

すると、面積が25c㎡の斜めの正方形を描けました。

しかし、ここで娘に学んでほしいのは斜めの正方形の描き方ではありません。
斜めの正方形の面積は7ｘ7－（（3ｘ4）÷2）ｘ4＝25c㎡です。二つの正方形を囲む大きな正方形の面積から4つの三角形の面積を引いて求めました。

下図ですが、差し引いた三角形のうち2つを移動しました。すると2つの正方形9c㎡と16c㎡が現れました。大きな正方形から三角形4つを取り除いた面積25c㎡と、2つの正方形9c㎡と16c㎡を合わせた面積は等しいですね。

すなわち・・・・
3cmｘ3cm＋4cmｘ4cm＝5cmｘ5cm
9＋16＝25
であることがわかります。
a^ ＋b^＝c^
になっていることがわかります。
最後にホワイトボードに書いておしまい。


なお、面積が10c㎡や20c㎡の場合でも上記の方法でで斜めの正方形を描画できます。
20c㎡＝2cmｘ2cm＋4cmｘ4cm の2つの正方形で構成されています。
10c㎡＝1cmｘ1cm＋3cmｘ3cmの2つの正方形で構成されています。